Thủy tĩnh học là một ngành học của thủy lực chuyên nghiên cứu về chất lỏng trong trạng thái tĩnh (mọi điểm trong chất lỏng đều đứng yên).
Một số trường hợp ngoại lệ có xét đến chất lỏng tĩnh đặt trên một hệ quy chiếu chuyển động thẳng có gia tốc hay chuyển động tròn đều.
Lực tác dụng cơ bản lên khối chất lỏng trong trường hợp này là trọng lực. Các thuộc tính khác như sức căng mặt ngoài, tính nhớt của chất lỏng thường ít được xét đến hơn.
Các bài toán trong thủy tĩnh học bao gồm:
- áp suất trong lòng chất lỏng
- áp lực lên một bề mặt đặt trong chất lỏng
- lực Ác-si-mét
- phương trình mặt thoáng và mặt đẳng áp
- sự nổi ổn định của vật trong chất lỏng
Các bài viết có thể xem thêm:
+ khái niệm động cơ
+ nguyên nhân của rủi ro tín dụng
+ Lợi ích của việc phát triển dịch vụ Ngân hàng Bán lẻ
TÓM TẮT
Các lực tác dụng lên chất lỏng
Trong môi trường chất lỏng tĩnh chất lỏng luôn chịu tác động của ngoại lực, như chúng ta đã biết được chia thành 2 loại: lực khối và lực mặt
– Lực khối : là các lực như trọng lực, quán tính
Gọi X, Y, Z là các lực khối đơn vị theo các phương Ox, Oy, Oz. Lực khối đơn vị là lực khối khi khối lượng bằng 1 kg. Ví dụ trường hợp vật rơi tự do lực khối đơn vị có độ lớn bằng gia tốc rơi tự do Z=9,8 N/kg.
Lực khối theo các phương
Mx=ρVX; My=ρVY; Mz=ρVZ.
– Lực mặt : là các lực tương tác giữa các phân tử chất lỏng hoặc giữa chất lỏng với các dụng cụ chứa. Đây chính là lực ma sát, gây nên đặc tính nhớt của chất lỏng.
Trong môi trường chất lỏng tĩnh, tức là không có sự chuyển động tương đối giữa các phân tử chất lỏng. Lực mặt trong trường hợp này sẽ không xuất hiện.
Như vậy trong môi trường tĩnh, chất lỏng chỉ chịu tác động của các lực khối.
Khái niệm áp suất thủy tĩnh
Ứng suất trong lòng chất lỏng sinh ra khi có ngoại lực tác dụng vào thì gọi là áp suất.
Trong trường hợp chất lỏng tĩnh, áp suất này được gọi là áp suất thủy tĩnh.
Biểu thức: p=F/S
F – là ngoại lực tác dụng, trường hợp tĩnh F là trọng lực và lực quán tính, N.
S – diện tích bề mặt chất lỏng chịu tác động của ngoại lực, m2.
Các tính chất của áp suất thủy tĩnh.
Tính chất 1: Tại một điểm bất kỳ trong lòng chất lỏng áp suất thủy tĩnh tác dụng thẳng góc với phần diện tích tiếp xúc của khối chất lỏng dược tách ra và hướng vào trong lòng khối chất lỏng đó.
Chứng minh:
Giả sử trong môi trường chất lỏng, ta xét một khối chất lỏng W. Tại phần diện tích rất nhỏ dS trên bề mặt của W, chịu tác động của áp suất p. Áp suất p tách ra thành hai thành phần: thành phần tiếp tuyến với dS là pt và thành phần pháp tuyến với dS là pn. Như ta đã biết trong trường hợp chất lỏng tĩnh, không có sự chuyển động tương đối giữa các phần tử chất lỏng hoặc chuyển động dương đối với bình chứa. Do đó thành phần theo phương tiếp tuyến pt=0. Khi đó p=pn.
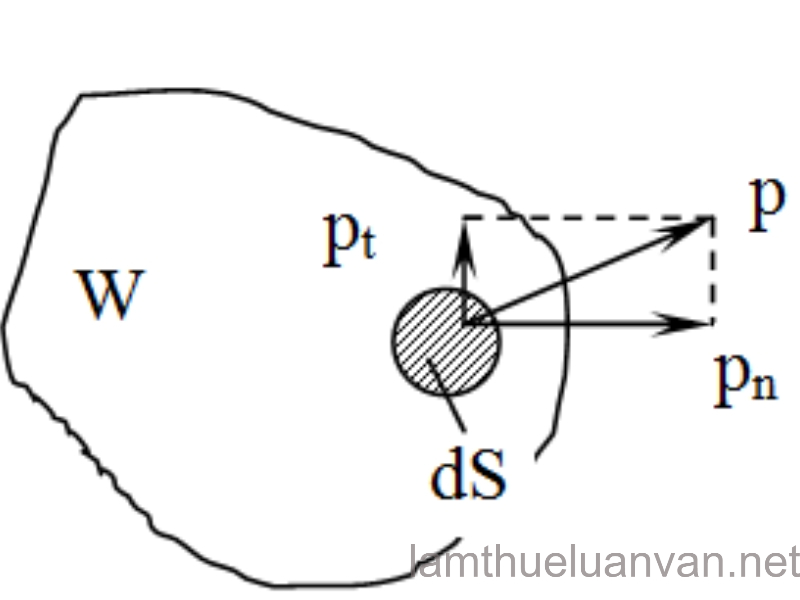
tính chất áp suất thủy tĩnh
Ta xét tới chiều của áp suất p. Sử dụng phương pháp loại trừ, ta thấy, p không thể hướng ra ngoài khối chất lỏng W được, vì nếu p hướng ra ngoài, phần diện tích dS sẽ có xu hướng bị kéo ra khỏi khối W, làm cho biến dạng khối W hay có sự chuyển động tương đối giữa các phần tử chất lỏng. Điều đó trái với điều kiện tĩnh của khối chất lỏng. Như vậy áp suất p chỉ có thể hướng vào trong khối chất lỏng.
Tính chất 2: Tại một điểm bất kỳ trong lòng chất lỏng áp suất thủy tĩnh theo mọi phương có giá trị như nhau.
Chứng minh:
Để chứng minh tính chất 2. Trong lòng chất lỏng tách ra khối chất lỏng có hình dạng tứ diện vuông ABCD với các cạnh là dx, dy, dz như hình vẽ. Trên cách mặt của tứ diện chịu tác động của các áp suất px, py, pz, và pn.
Giả sử tứ diện đủ nhỏ để coi như các áp suất tác dụng lên các mặt tứ diện phân bố đều. Theo tính chất 1 thì các áp suất tương ứng vuông góc các mặt tứ diện và hướng vào trong lòng tứ diện như hình vẽ.
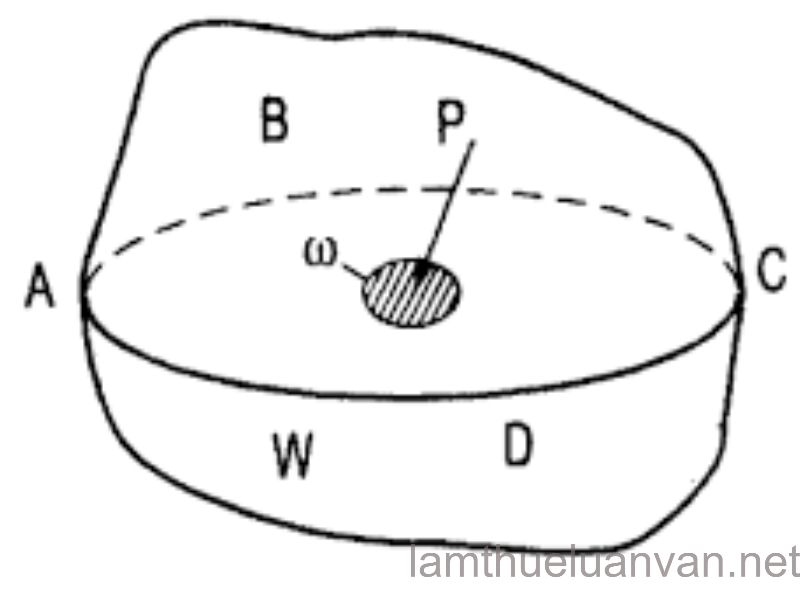
Áp suất thủy tĩnh
Ta đi tìm biểu quan hệ giữa các áp suất trên các mặt của tứ diện.
Khối chất lỏng nằm cân bằng. Chúng ta thiết lập phương trình cân bằng lực.
Chất lỏng tĩnh vậy tác động lên khối chất lỏng có áp lực ở các cạnh và lực khối.
Xét cân bằng trên phương Ox. Ta có
pxSACD – pnSBCD cos(n,x)+ρVABCDX=0
hay pxdydz/2 – pnSBCD cos(n,x)+ =0
Mà SBCD cos(n,x)=SACD= dydz/2
Suy ra: px – pn + ρdxX/3=0
Khi dx à 0 tức là tiến về điểm A thì px=pn.
Vậy tại điểm A ta có px=pn.
Tương tự cũng chứng minh được tại điểm A có px=py=pz=pn.
Tính chất 2 được chứng minh.
Tính chất 3 : Áp suất thủy tĩnh tại một điểm phụ thuộc vào tọa độ trong không gian của điểm đó.
p=f(x,y,z)


